Width and length of a slit images: grating magnification

The relation between the silt width and its image width is described as follows,

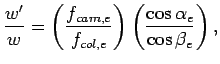$$\frac{w^{\prime}}{w} = \left( \frac{f_{cam,e}}{f_{col,e}} \right) \left( \frac{\cos \alpha_e}{\cos \beta_e} \right) ,$$ (18)

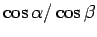The $\cos \alpha / \cos \beta$ is called ``anamorphic magnification'' (Chaffee & Schroeder, 1976) or ``grating magnification'' (Wheeler, 1973). The width of a slit image increases with increasing grating magnification. Since the diffraction angle increases with wavelength, the width of a slit image becomes wider with increasing wavelength.

The length of the slit image is adopted in the same way. Since the dispersion of the cross-disperser is along the direction of the slit, the grating magnification of cross-disperser is adopted. The length of the slit image can then be written as

$$l^{\prime} = \frac{ l \left( \frac{f_{cam}}{f_{col}} \right) \left( \frac{\cos \alpha}{\cos \beta} \right) } {\cos \chi} .$$ (19)

where we take into account the tilt of the slit. The slit length magnification affects the pixel scale along the direction of the slit length.

Variations of the slit area and shape cause intensity variation and continuum contamination. For a uniform intensity source, the intensity per pixel will be affected by the grating magnification. This effect can be corrected by taking spectra of spectrophotometric standard stars that have flat continuum and weak spectral lines observed with the same spectrograph configuration as target objects.